In surveys and polls it is common to use
stratified sampling. Stratified sampling is also used in data mining, when drawing a sample from a database (for the purpose of model building). This post follows an active discussion about stratification that we had in the "Scientific Data Collection" PhD class. Although stratified sampling is very useful in practice, the explanation of why to do it and how to do it usefully is not straightforward; this stuff is only briefly touched upon in basic stats courses. Looking at the current Wikipedia entry further supports the knowledge gap.
What is stratifying? (that's the easy part)Let's start by mentioning what an ordinary (not stratified) sample is: a "simple random sample" of size
n means that we draw
n records from the population at random. It's like drawing the numbers from a bag in Bingo.
Stratifying a population means dividing it into non-overlapping groups (called strata), where each unit in the population belongs to exactly one stratum. A straightforward example is stratifying the world's human inhabitants by gender. Of course various issues can arise such as duplications, but that's another story. A stratified (random) sample then means drawing a simple random sample from each stratum. In the gender example, we'd draw a simple random sample of females and a simple random sample of males. The combined samples would be our "stratified sample".
Why stratify?The main reason for stratifying is to
improve the precision of whatever we're estimating. We could be interested in measuring the average weight of 1-year old babies in a continent; the proportion of active voters in a country; the difference between the average salary of men and women in an industry; the change in the percent of overweight adults after opening the first MacDonalds in a country (compared to the percent beforehand).
Because we are estimating a population quantity using only a sample (=a subset of the population), there is some inaccuracy in our sample estimate. The average weight in our sample is not identical to the average weight in the entire population. As we increase the sample size, a "good" estimate will become more precise (meaning that its variability from sample to sample will decrease). Stratifying can help improve the precision of a sample estimate without increasing the sample size. In other words, you can get the same level of precision by either drawing a larger simple random sample, or by drawing a stratified random sample of a smaller size. But this benefit will only happen if you stratify "smartly". Otherwise there will be no gain over a simple random sample.
How to stratify smartly?This is the tricky part. The answer depends on
what you are trying to measure.
If we are interested in an
overall population measure (e.g., a population average, total or proportion), then the following rule will help you benefit from stratification:
Create strata such that each stratum is homogeneous in terms of what's being measured. Example: If we're measuring the average weight of 1-year-old babies in a continent, then stratifying by gender is a good idea: The boys' stratum will be more homogeneous in terms of weight compared to mixing boys and girls (and similarly the girls' stratum will be homogeneous in terms of weight). What are other good stratifying criteria that would create groups of homogeneous baby weights? How about country? the parents' weights?
If we are interested in
comparing measures of two populations, then the same idea applies, but requires more careful consideration:
Create strata such that each stratum is homogeneous in terms of the difference between the two population measures.Example
: To compare the % of overweight adults in a country before and after opening the first MacDonalds, stratification means finding a criterion that creates strata that are homogeneous in terms of the difference of before/after weight. One direction is to look for populations who would be affected differently by opening the MacDonalds. For example, we could use income or some other economic status measure. If in the country of interest MacDonalds is relatively cheap (e.g., the US), then the weight difference would be more pronounced in the poor stratum; in contrast, if in the country of interest MacDonalds is relatively expensive (e.g., in Asia), then the weight difference would be less pronounced in the poor stratum and more pronounced in the wealthy stratum. In either country, using economic status as a stratifying criterion is likely to create strata that are homogeneous in terms of the difference of interest.
In data mining, taking a stratified sample is used in cases where a certain class is rare in the population and we want to make sure that we have sufficient representation of that class in our sample. This is called over-sampling. A classic example is in direct mail marketing, where the rate of responders is usually very low (under 1%). To build a model that can discriminate responders from non-responders usually requires a minimum sample of each class. In predictive tasks (such as predicting the probability of a new person responding to the offer) the interest is not directly in estimating the population parameters. Yet, the precision of the estimated coefficients (i.e., their variance) influences the predictive accuracy of model. Hence, oversampling can improve predictive accuracy by again lowering the sampling variance. This conclusion is my own, and I have not seen mention of this last point anywhere. Comments are most welcome!
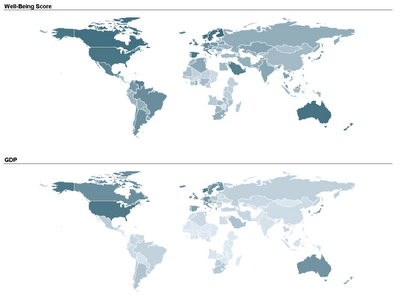 Another team used a map to compare nursing homes in the US, in terms of quality of care scores. Their map below show the average quality of nursing home in each US State (darker means higher quality).
Another team used a map to compare nursing homes in the US, in terms of quality of care scores. Their map below show the average quality of nursing home in each US State (darker means higher quality).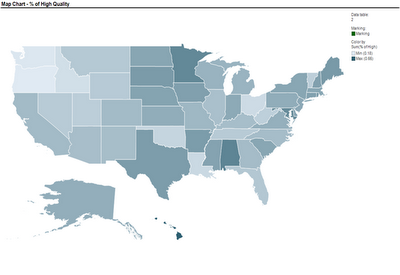 These two sets of maps were created using TIBCO Spotfire. Following many requests, here is an explanation of how to create a map chart in Spotfire. Once you have your ordinary data file open, there are 3 steps to add the map component:
These two sets of maps were created using TIBCO Spotfire. Following many requests, here is an explanation of how to create a map chart in Spotfire. Once you have your ordinary data file open, there are 3 steps to add the map component: